Glider-Guns in 3d Cellular Automata
Discrete Dynamics Lab
| |
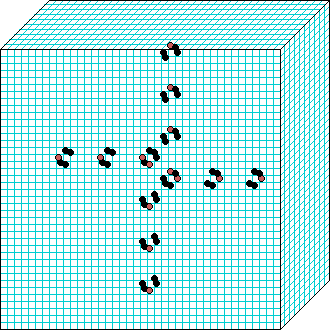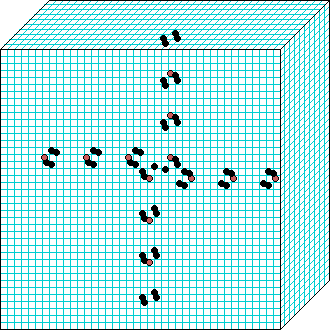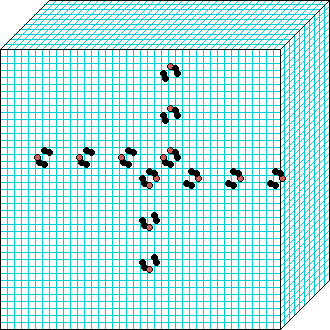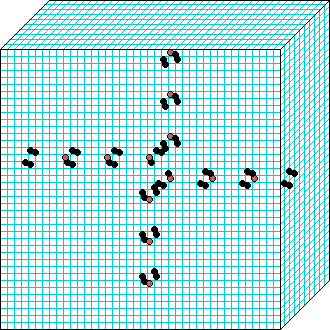 k=6 Beehive-rule period=6 | | | 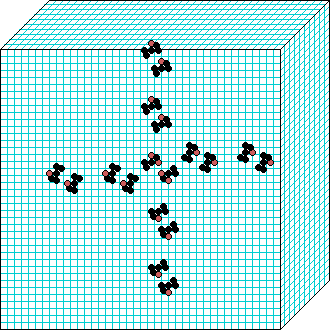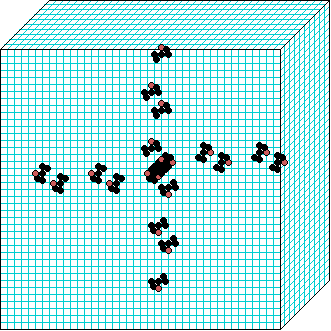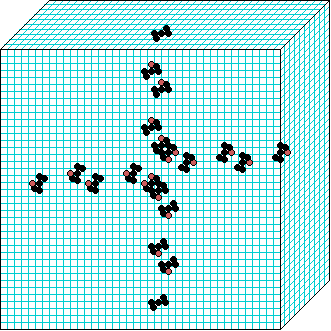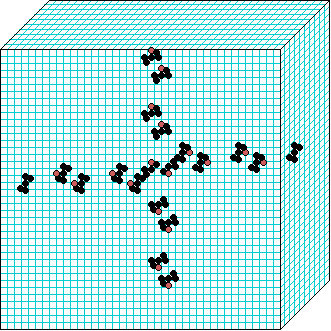 k=7 Spiral-rule period=8 |
|
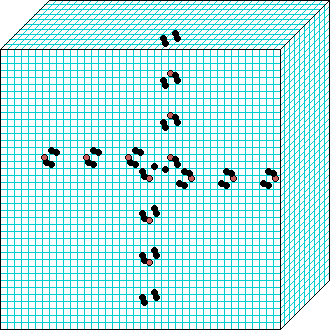
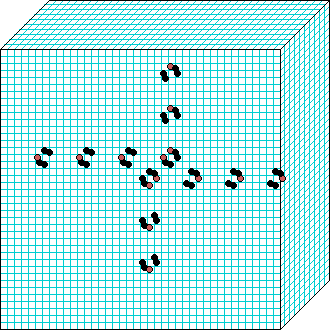
Beehive-rule
3d glider-gun v=3 k=6 ijh=40x10x40 -- click panels to enlarge kcode= 0022000220022001122200021210=(hex)0a0282816a0264 (v3k6x1.vco in DDLab) "Glider dynamics in 3-value hexagonal cellular automata: the beehive rule", Int.J.Unconv.Comp, Vol.1, No.4, 2005, 375-398. (PREPRINT) | ||||||
|
|
|
|

|

| ||
| | | | | | | ||
|
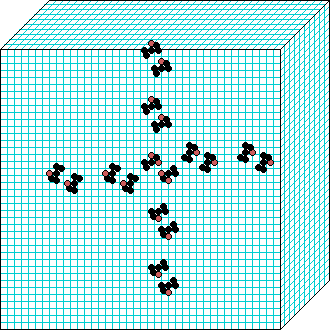
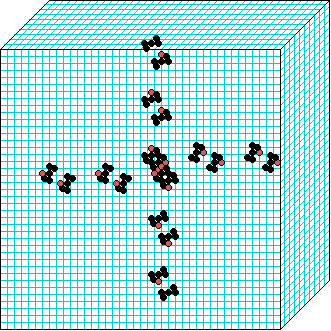
Spiral-rule
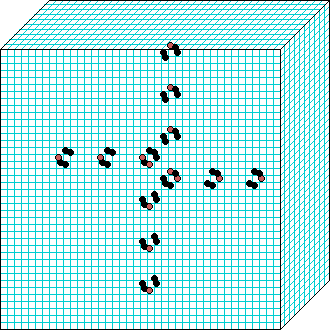
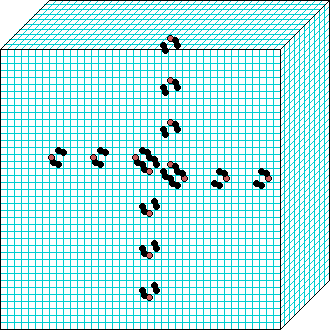
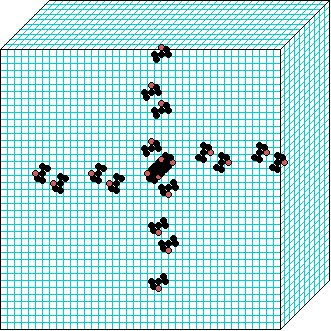
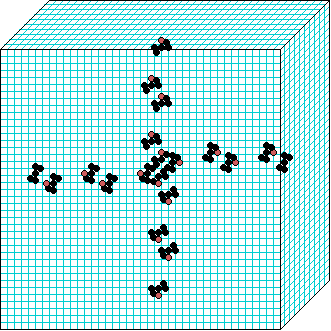
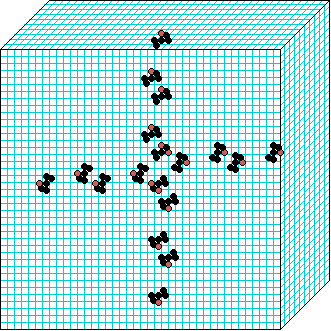
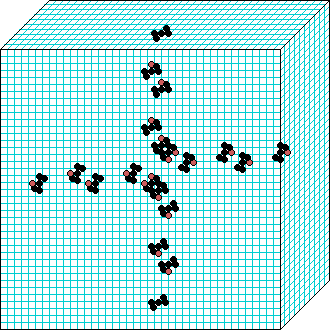
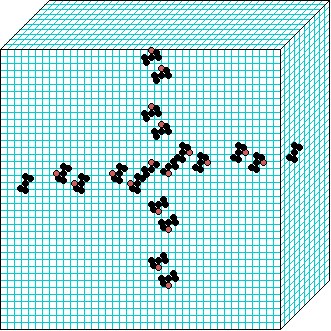
3d glider gun v=3 k=7 ijh=40x10x40 -- click panels to enlarge kcode=000200120021220221200222122022221210=(hex)020609a2982a68aa64 (v3k7w1.vco in DDLab) "On spiral glider-guns in hexagonal cellular automata: activator-inhibitor paradigm" Int.J.Mod.Phys C, Vol. 17, No. 7,1009-1026, (PREPRINT) | ||||||||
|
|
|
|
|
|

|
| ||
| | | | | | | | | ||
In these examples, imagine looking down into a shallow box 40 x 40, and 10 cells deep.
Periodic boundaries have been suppressed so that
the gliders fall out of the space so an not to interfere with the generating core.
The 3d glider-guns are periodic structures fixed in one location, which spontaneously
emerged in the dynamics from random initial states. The CA rules
are identical to the
k-totalistic
rules -- beehive and spiral,
but apply to a 3d (nearest neighbour) cubic neighbourhood. Because k-totalistic rules are
symmetric -- independent of the location of values in the neighbourhood --
the glider-guns exist in each chirality and in all
possible orientations. Many other structures also emerge --
gliders, compound-gliders, and mobile glider-guns, but as yet no
static structures analagous to 2d eaters in the 2d
spiral rule. I
discovered the 3d glider-gun in the beehive-rule in 2004, and in the
spiral-rule in June 2009. The best way to search for these structures
is to set a small random 3d block in DDLab, 2 or 3 cells in diameter,
and observe the result. The core of the glider-gun can then be
isolated (and saved) with other DDLab methods.
back to the
DDLab home page
Last modified: June 2009